Controls

Click on a vertex (circle, triangle, square) to play there. 
h: hint 
m: switch between dragging vertices and making moves 
n: new game

Rules

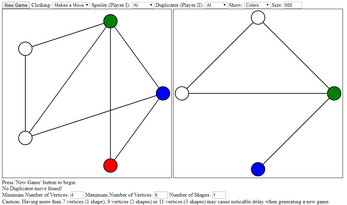
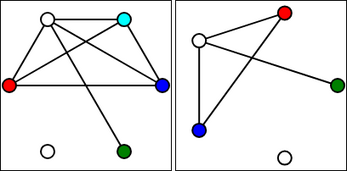
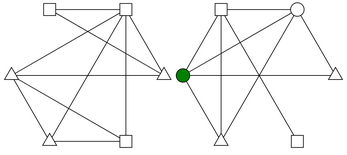
The Ehrenfeucht-Fraïssé Game is a game about first order logic and the inevitable end of all things. Players take turns matching up the vertices (shown as circles, etc.) of two graphs (networks):

1. First, Player I (Spoiler) selects a vertex from either graph that has yet to be selected, and colors it a new color.
2. Next, Player II (Duplicator) selects a vertex from the other graph that has yet to be selected, and colors it the same color, forming a match between the two vertices of that color.

The game ends if either:

• Two vertices that are connected by an edge (line) in one graph are matched with vertices which are not connected in the other.
• A vertex of one shape gets matched with a vertex of another shape.
• Or, there are no more vertices left to pick.

The game will inevitably end. Spoiler's (Player I's) goal is to end the game as quickly as possible. Duplicator's (Player II's) goal is to last as long as possible.

• The Duplicator AI is currently a poor sport and will simply forfeit if it cannot find a suitable match.
• Most versions of the game allow Spoiler to pick previously selected vertices, so long as they are matched with the vertex the original vertex was matched to. Since Spoiler, in seeking to end the game as quickly as possible, has no reason to do this, it is disallowed.

Read More

You can learn more about Ehrenfeucht–Fraïssé Games at:

• Cornell Math Explorers' Club
• Stanford Encyclopedia of Philosophy

You can also see my attempt to make a version of this for finite linear orderings in 100 hours at: https://trkern.itch.io/efglo. Stay tuned for more weird math games!